Alongside Orthogonal Beamforming (OBF) and Functional Beamforming (FBF), the MUSIC algorithm presents an alternative extended opportunity to increase the dynamic range and improve source localization when analyzing tonal or low-frequency sound sources. Analogous to OBF, MUSIC is working with Beamforming based on the (covariant) Cross Spectral Matrix (FDBF) while a decomposition referring to its eigenstructure is conducted and the latter is sorted by the sizes of the eigenvalues.
Decomposition into two subspaces can be conducted by the help of the eigenvectors associated with the Cross Spectral Matrix (CSM): the signal subspace (selected components in NI) and its complement associated with microphone noise. From experience, the number of selected components is best adjusted to half the number of microphones.
Based on this decomposition, the MUSIC algorithm assumes the noise-associated eigenvectors and a steering vector to be orthogonal when the steering vector location and the actual source location coincide. The formulation of the beamforming result is introduced in the FAQ MUSIC - Mathematics.
MUSIC especially shows its strengths when analyzing tonal sound sources in acoustically non-perfect environments and when localizing low-frequency sound sources. Due to the principle, absolute sound levels cannot be depicted since the beamforming solution does not contain any information given by the eigenvalues and thus the source strength.
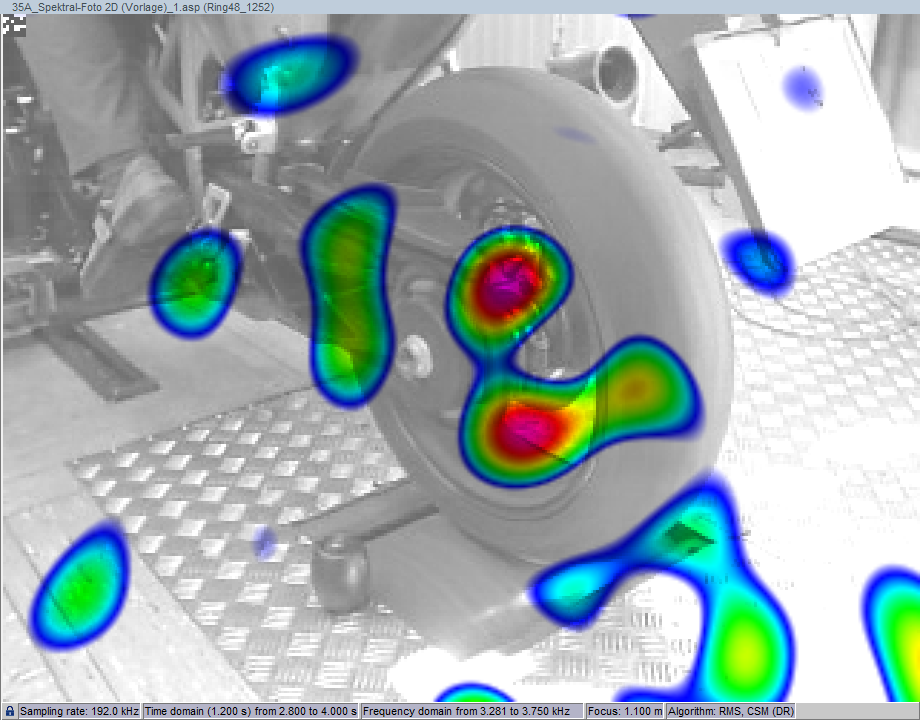
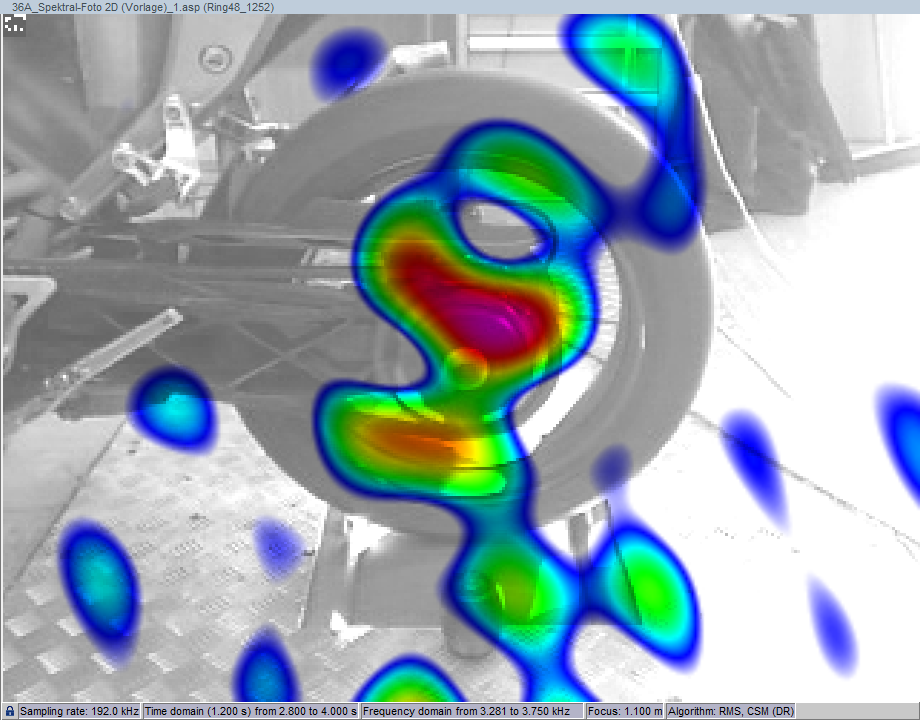
Application Example: Motorcycle
In the example of a motorcycle on a test stand, the frequency range of 3.28 kHz to 3.75 kHz is analyzed. MUSIC in comparison to FDBF clearly improves the localization of the most important sound sources and increases the dynamic range.
R. O. Schmidt, "Multiple emitter location and signal parameter estimation" IEEE Trans. Antennas Propag., vol.AP-34, pp. 276-280, March 1986.
Visit the website Berlin Beamforming Conference held by GFaI e. V. https://www.bebec.eu.
