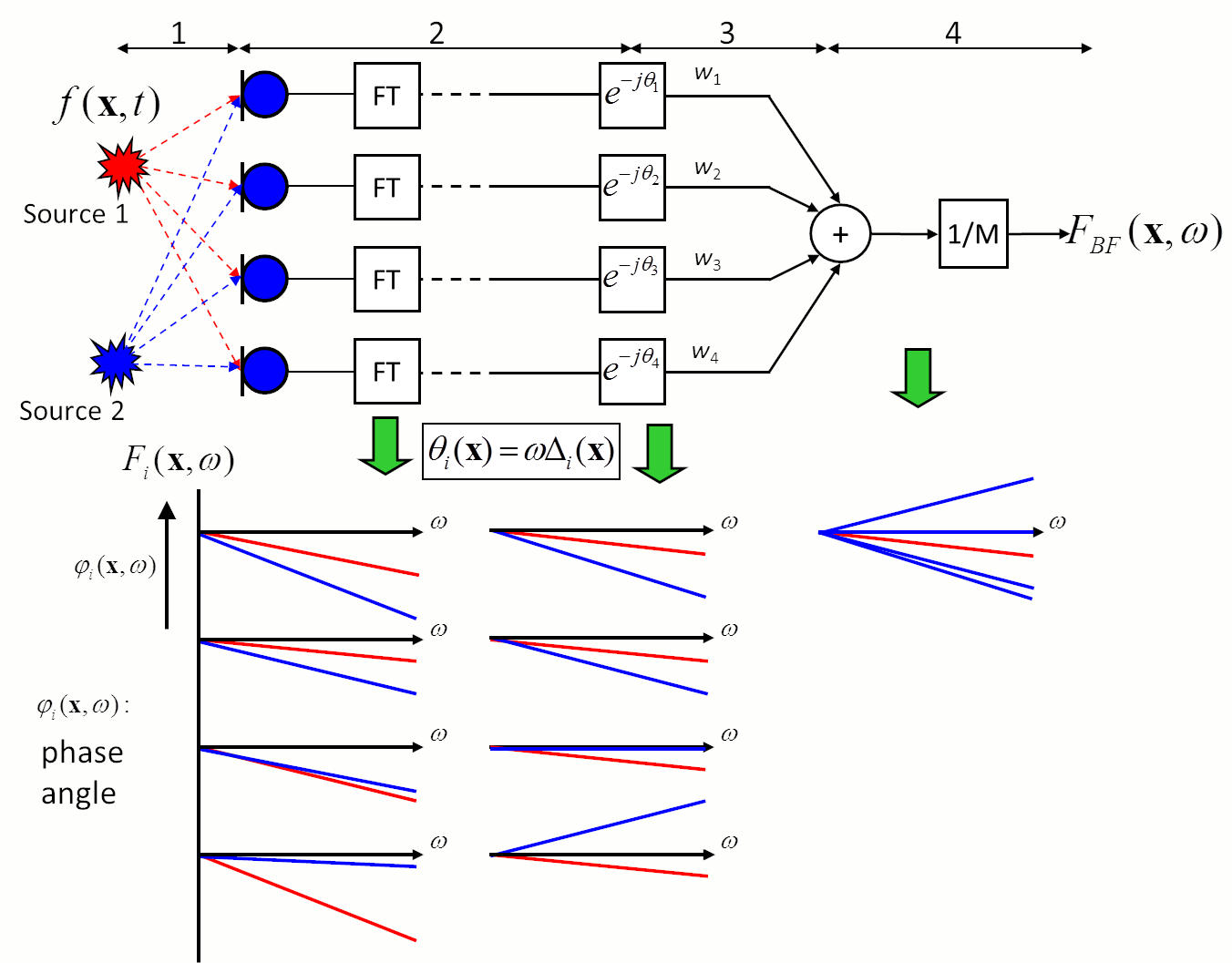
The Delay-and-Sum Beamformer in frequency domain is based on a similar principle as in time domain. The block diagram in Fig. 1 illustrates the case of two point sources situated in a measurement plane in front of the microphone array.
- The sound of each source travels to each of the microphones along different paths. This leads to delays and phases in the measured signals, which are both proportional to the travelled distances. The delays can be determined from the known distance between the microphone array and the measurement plane and the speed of sound.
- After performing the Fourier transform of each microphone signal, the spectra are available as amplitude and phase. Now, the phase of each individual microphone signal can be corrected with respect to a particular delay. It is multiplied by a complex phase term without influencing the amplitude. An example of this procedure is presented in Fig. 1. Here, the phasing of the signal parts is carried out to the target Source 1. As a result, the signal parts of Source 2 are out of phase. It is important to note that a constant time delay results in a frequency dependent phase correction term.
- The resulting complex spectra are added up. In this process, the signal parts of Source 1 add up constructively and the signal parts of Source 2 diminish.
- Finally, the summed signal is normalised by the number of microphone channels. From the sum spectrum the RMS and the maximum value can be calculated and visualized in the acoustic map.
To auralise the sound signal at a focus point, it is possible to perform the inverse Fourier transform resulting in the local time Signal \(f_{BF}(x,t)\) at the focus point.