Korrelationsfilter

Was kann mit dem Korrelationsfilter erreicht werden?

Unter dem Begriff Korrelation versteht man in der Signalverarbeitung die Ähnlichkeit zweier Signale. Mit dem Korrelationsfilter lassen sich die mit einer bestimmten Referenz korrelierten Anteile entfernen oder isolieren. So besteht bei der Aufzeichnung von Signalen mit einem Mikrofonarray die Möglichkeit, einen oder mehrere Referenzkanäle aufzunehmen. Alternativ können diese auch aus einer akustischen Karte generiert oder als Audiodatei importiert werden. Unabhängig von der gewählten Methode zur Bestimmung des Referenzkanals bleibt die damit verbundene Zielsetzung ähnlich: die Auswirkung des Referenzsignals und der darin enthaltenen Quellen auf die gesamte akustische Karte zu untersuchen.

Es wird angenommen, dass sich das Signal $x_{mic}(t)=x_{uncorr}(t)+x_{corr}(t)$ aus einem vom Referenzsignal $x_{ref}(t)$ unabhängigen Anteil $ x_{uncorr}(t)$ und einem mit dem Referenzsignal korrelierten Anteil $x_{corr}(t)$ darstellen lässt.

Für $ x_{corr }(t)$ wird wiederum angenommen, dass es sich aus einer Summe von zeitlich verschobenen und in der Amplitude skalierten Wiederholungen des Referenzsignals zusammensetzt (z. B. durch Mehrfachreflexionen): $$x_{corr}\left(t\right)=\ \sum_{n=1}^{N}{\alpha_n\cdot x_{ref}(t-\tau_n)}$$

Aus dem Betrag der Korrelationsfunktion zwischen $x_{mic}(t)$ und $x_{ref}(t)$ wird der Zeitversatz $τ_n$ bestimmt, der am Ort des größten lokalen Maximums liegt. Anschließend wird der zugehörige Faktor $∝_n$ mit einem Optimierungsverfahren ermittelt. Auf diese Weise lässt sich der korrelierte Anteil aus dem Signal isolieren, wobei die $N$-malige Wiederholung dieses Vorganges mit dem verbleibenden Signal der Filterordnung $N$ bzw. Anzahl der Iterationen entspricht. Abhängig von dem gewählten Modus des Korrelationsfilters wird am Ende entweder $x_{ corr }(t)$ oder $x_{ uncorr }(t)$ vom ursprünglichen Mikrofonsignal $x_{ mic }(t)$ entfernt.

Anwendungsbeispiel: Lautsprecher

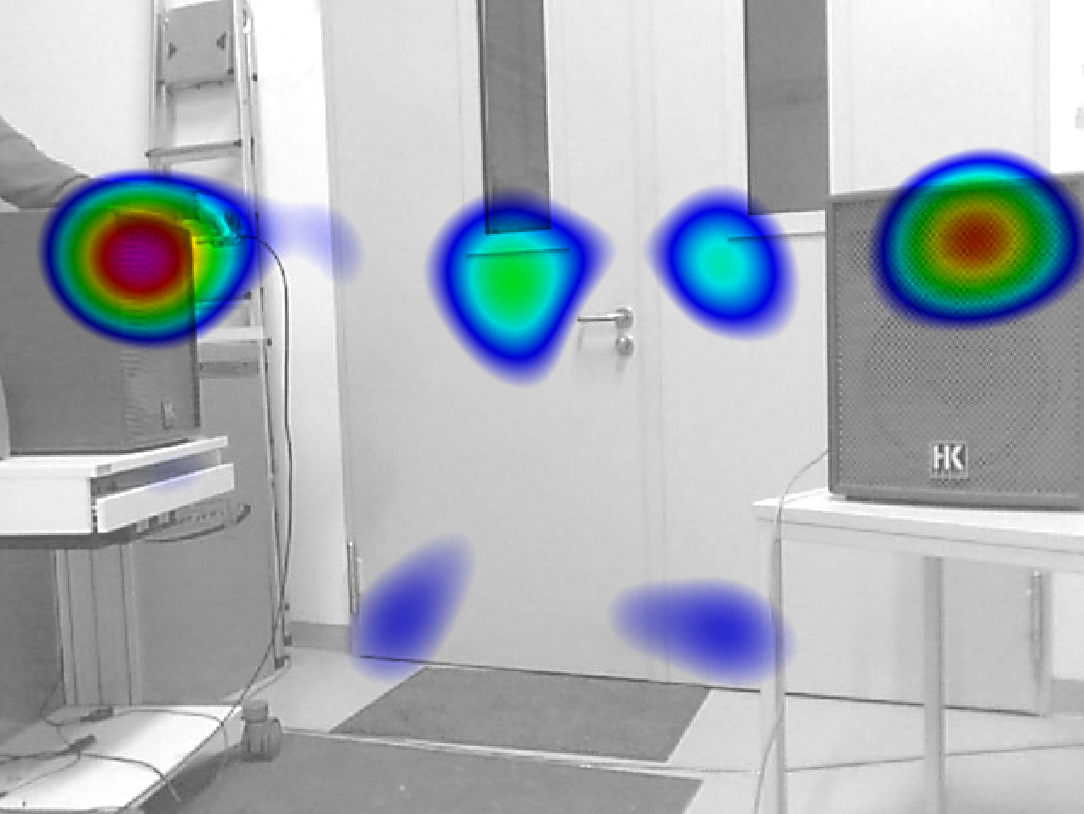
Abbildung 1 zeigt die akustische Karte zweier Lautsprecher im 8-kHz-Terzband, die jeweils inkohärente Signale (nicht phasengleich und nicht frequenzgleich) ausstrahlen. Dazwischen zeigen sich mehrere Schallquellen, bei denen es sich vermutlich um eine Reflexion des linken Lautsprechers handelt. An diesem Lautsprecher wird auch das Referenzsignal mit einem Mikrofon aufgezeichnet. In Abbildung 2 ist die akustische Karte der korrelierenden Anteile für die Filterordnung $N=10$ zu sehen, während Abbildung 3 die nichtkorrelierenden Anteile mit $N=45$ zeigt. Daraus lässt sich schließen, dass die Schallquelle am linken Türflügel unterhalb des Fenster mit dem linken Lautsprecher korreliert, was die Vermutung bestätigt, dass es sich hierbei um eine Reflexion handelt. Alle akustischen Karten wurden mit dem Funktionalen Beamforming mit $ν=4$ berechnet.