Point-Spread Function

An isotropic acoustic source is assumed to radiate under free field conditions at the location \( \vec{x_0} \). However, when mapped using a beamforming-approach, the resulting map \( F_{\vec{x_0}}(\vec{x} \)) will not display an ideal point. Moreover, the map will show additional sources next to \( \vec{x_0} \) that don't exist in reality. This effect results from spatial undersampling of the beamformer because its resolution is limited by a finite number of microphone positions. As a consequence, an acoustic photo can never be a perfect mapping of a sound event. The map \( F_{\vec{x_0}}(\vec{x} \)) is also known as the point spread function of \( \vec{x_0} \). It is an important basis for the evaluation of acoustic photos and for the design of microphone arrays.

Point-Spread Function

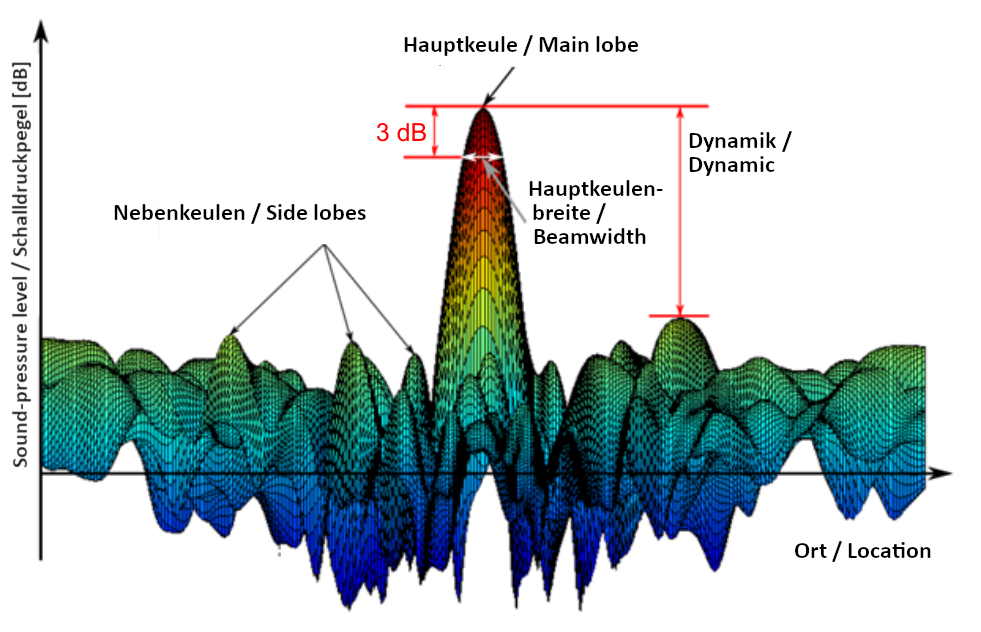
In general, the point spread function (PSF) characterizes the response of a system to a point source. For beamforming, Figure 1 illustrates an example of a PSF by plotting the sound pressure against the location. The global maximum is called the main lobe. Further maxima - resulting from the effect mentioned earlier - are called side lobes. The characteristics of main and side lobes are fundamental for the evaluation of an acoustic photo. Therefore, we need to explain the terms for describing them:

Beamwidth

The beam width [m] is the width of the global maximum at a level of -3 dB beneath its peak value. Based on this notion, it is possible to quantify the minimal distance of neighbouring sources which is needed for the beamformer to be able to distinguish them.

Dynamic

The dynamic [dB] characterizes the gap between the sound pressure of the main lobe and the sound pressure of the loudest side lobe. Knowledge about the dynamic is the key for identifying sources that are caused by undersampling: If an acoustic photo is displayed with a contrast which is equal or higher than the dynamic of a PSF, it is not possible to distinguish between real sources and side lobes.