Influence of Windowing

Figure 1 shows an acoustic map (TDBF) containing two loudspeakers, which transmit time-shifted impulse signals. Figure 2 shows an acouctic map computed with FDBF but under the same conditions as in time domain (0-96 kHz).

The results are different: Using FDBF in Figure 2, only one source has been identified. For the computation of the FDBF map, a “short-time fast Fourier Transform” was used. Therefore, the signal was divided in fixed parts and multiplied with an arbitrary window function.

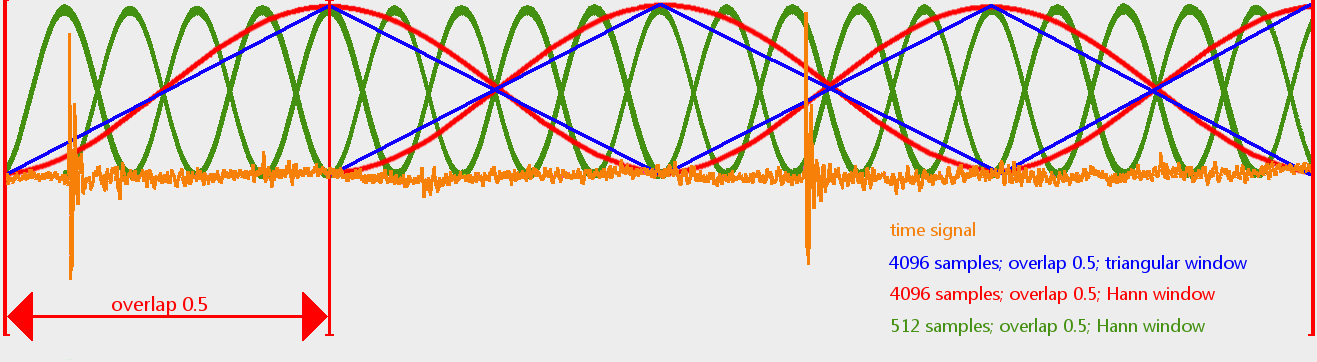
Figure 3 features a sequence of the original signal (orange graph), which was used to calculate the acoustic maps depicted in Figure 1 and 2. In order to preserve the clarity of the representation, only the signal from one channel is illustrated.

Using a window size of 4096 samples and a Hann window (red graph in Figure 3), the first impulse of the discrete signal is damped. Unfortunately, this information is not longer available or further calculations with the FDBF algorithm. The same problem occurs with the triangular window function (blue) and same window size of 4096 samples. As a result, the first loudspeaker can not be localized in Figure 2.

In order to prevent this effect, the parameters should be checked and the window size should be adapted, e.g. to 512 samples (green line in Figure 3). The first signal’s amplitude is substantially less damped - compared to the previously chosen window size. Here, the FDBF algorithm considers all information of the original signal and the acoustic map is identical to the one shown in Figure 1.

To avoid this type of error, it is recommended to use a Hann window for the Fourier Transform and expand the window by a half at both ends, before and after the range of interest.