Many post-processing beamforming algorithms rely on the Cross Spectral Matrix (CSM) or, more accurately, the cross power spectral density matrix. The Power Spectral Density (PSD) of a signal \(x(t)\) describes its power distribution over the frequency. In the frequency domain, this is given by the (normalized) square of the magnitude after Fourier transformation of the input signal.
Similarly, the cross-power spectral density of discrete signals \(x(t)\) and \(y(t)\) is defined as
$$PSD_{xy}(f) = \frac{1}{T}DFT(x(t))\cdot DFT^*(y(t))$$
where DFT stands for discrete Fourier transform, T for the time period and * indicates the complex conjugate. The cross power spectral density, analogue to a time domain cross-correlation, is used in signal processing to estimate the degree of correlation between two signals.
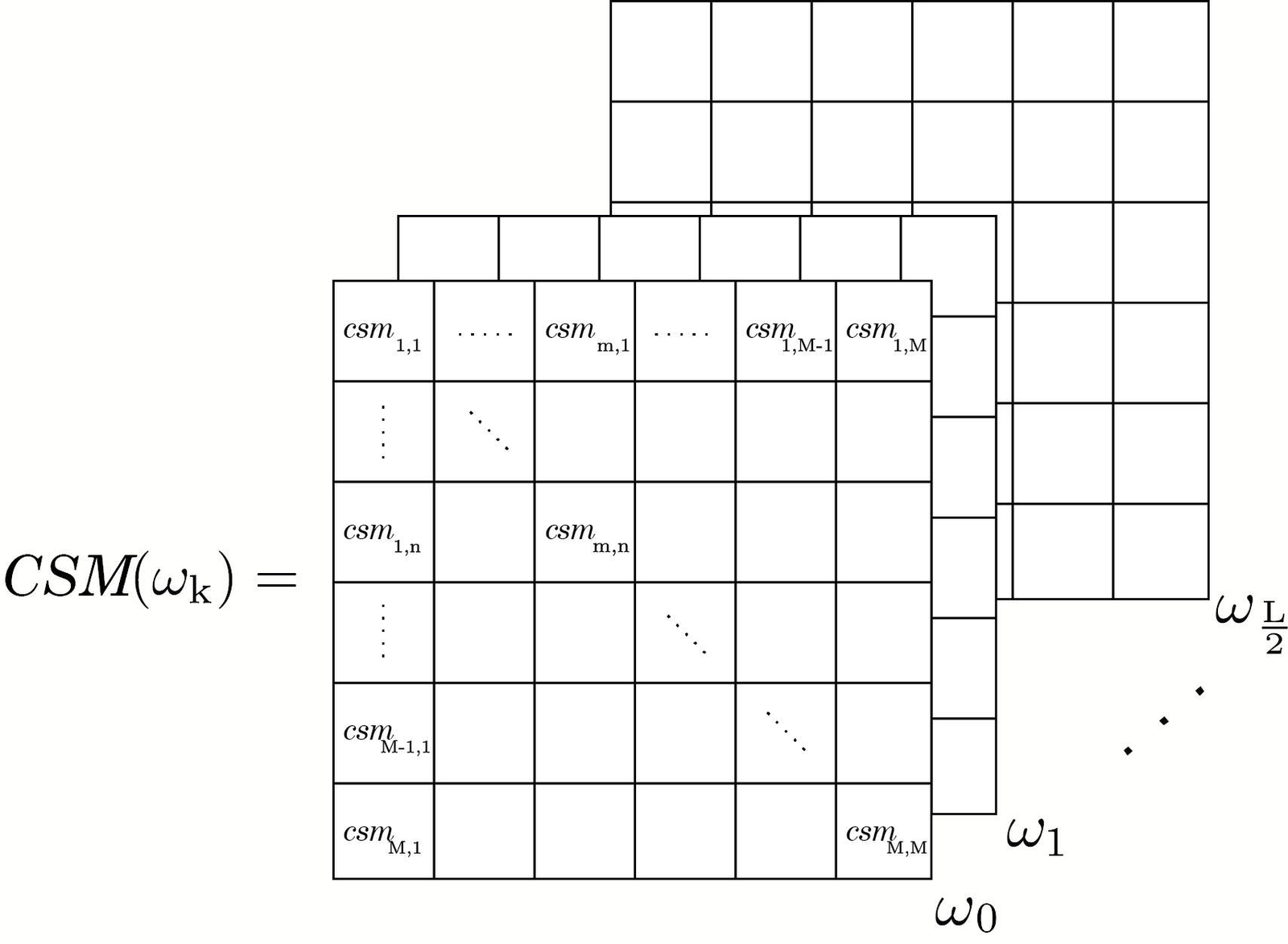
The CSM is constructed storing the cross-power spectral densities of each microphone couple combination (along with their complex conjugates and including the auto-power spectra of each microphone in the diagonal) for all frequencies in the spectrum of interest. A 3D-diagram of this matrix is depicted in figure 1, where m and n represent the microphone indexes, M the number of microphones, ω the angular frequency and L the chosen block length. The hermitian CSM allows a compact management of the data for further advanced post-processing, e.g. CLEAN-SC, SODIX, MUSIC, Orthogonal beamforming, etc.
Visit the website Berlin Beamforming Conference held by GFaI e. V. https://www.bebec.eu.
