Adaptation of FE Simulation of a Flange Component to Measured Modal Results by Means of Finite Element Model Updating

Finite Element Model Updating (FEMU) was applied to the model of a blind flange to improve FE simulation accuracy. Model updating is used to optimize the accuracy of the initial FE model so that the predicted dynamic behavior matches as closely as possible that observed through experiment. Finite Element Analysis (FEA) on the structure was therefore performed in parallel with Experimental Modal Analysis (EMA) on the original component.

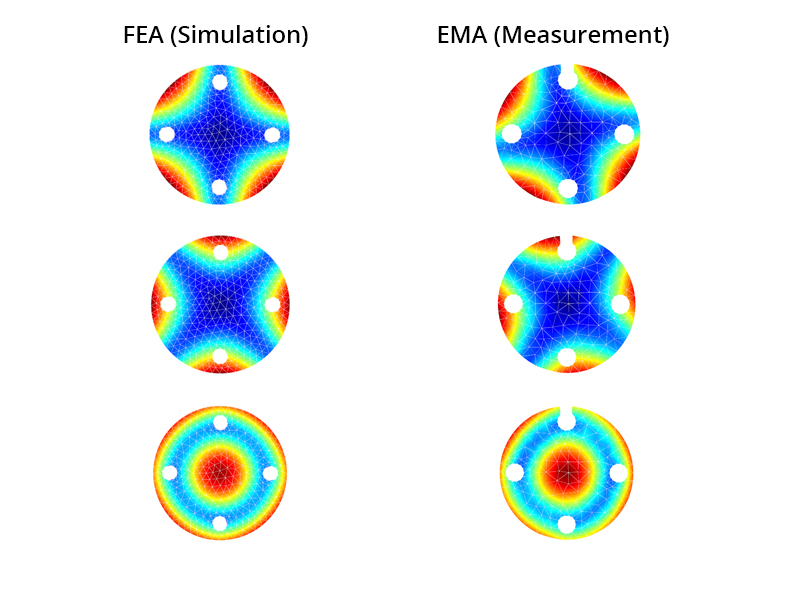
With the aid of a solid model identical to the original component, the input of the specific material properties of stainless steel and the imposition of free boundary conditions, it was possible to create a corresponding FE model (Figure 1, left) for the FEA. Numerical calculation of the modal parameters yielded the natural frequencies listed in Table 1 (left) and the vibration modes associated with them in Figure 2 (left column) for the first three natural modes of the structure. To optimize the simulative results, the modal values from an experiment were to be obtained using the real structure. For this purpose, the flange was elastically suspended from a profile frame to simulate the assumed free boundary conditions from the FE simulation. A wide-band excitation of the structure was performed by a coupled modal shaker on the rear side, while the structural responses were recorded at more than 200 measurement points by a laser scanning vibrometer (LSV) (Figure 1, right).

Figure 1: FE model of the blind flange consisting of over 4000 elements (left), experimental setup of the EMA (right). Wideband excitation of the structure by a modal shaker. Acquisition of the system responses by means of LSV.
Figure 1: FE model of the blind flange consisting of over 4000 elements (left), experimental setup of the EMA (right). Wideband excitation of the structure by a modal shaker. Acquisition of the system responses by means of LSV.
Figure 2: Showing normalized mode shapes at 4786, 4975 and 7858 Hz from FEA (left column), mode shapes of identified natural frequencies at 4607, 4781 and 7593 Hz from EMA (right column).
Figure 2: Showing normalized mode shapes at 4786, 4975 and 7858 Hz from FEA (left column), mode shapes of identified natural frequencies at 4607, 4781 and 7593 Hz from EMA (right column).

From the measured vibration data, the natural frequencies listed in Table 1 (center) could be determined for the first three natural modes in the further modal analysis.

The corresponding vibration modes are shown in Figure 2 (right).

Table 1: The determined natural frequencies of the FEA before and after the optimization by the Model Updater, as well as those of the EMA
FEA (Hz)Δ(%)EMA (Hz)FEAoptimized (Hz)Δ(%)
47863,9460746100,1
49754,1478147920,2
78583,5759375680,3

In the model updating, these experimentally determined measurement data are now used to update the simulated values with respect to selected structural parameters (e.g. elastic modulus, mass density) in the FE model and to adjust them accordingly. This results in the optimized values of the natural frequencies shown in Table 1 (right), which deviate by a maximum of 0.3 % from those determined from the EMA. Before updating, the natural frequencies were calculated with up to 4.1 % deviation.

The optimized model allows the structural behavior to be modeled more accurately, e.g. for changed load conditions or the influence of specific modifications on the modal parameters.  Accuracy and reliability can thus be significantly increased.

In addition, the optimized model can also be used as a basis for identifying potentially plant-critical operating conditions in order to counteract potential material failure at an early stage.

Quick Access