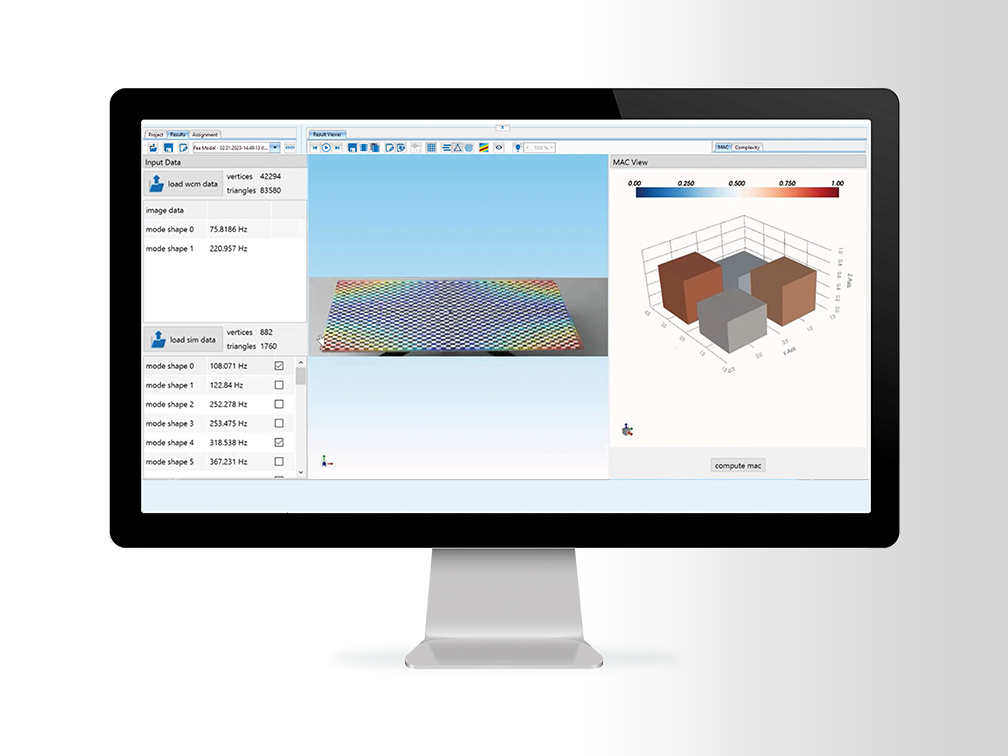
Finite Element Analysis (FEA) is a powerful tool to predict the dynamic vibration behavior of any kind of structure numerically. Based on the structural geometry, the specification of material properties and the imposed boundary conditions, the modal parameters (natural frequency, mode shape and damping) of the structure can be calculated. This method thus forms an important instrument in component and structure development (e.g. digital prototyping), which is mainly reflected in a shortened product development time.
The FEA module provides different algorithms to identify modal parameters (FEA Modal), simulate the structures static stress and strain (FEA Static), predict the structures dynamic answer to different external loads (FEA Transient) and calculate frequency response functions (FEA Frequency Response). Additionally the simulation model can be enhanced with real world measurements based on WaveCam measurements using the FE Model Updating functionality.
This helps with planning, construction and maintenance. New designs, changes to the structure and external loads can be precisely simulated and optimized. This powerful tool assists you in your development process and prototyping to identify operation-critical or troublesome resonant frequencies of the structure and to gain a clear understanding of the cause-and-effect relationships between specific vibration excitations and their response.
Simulation needs only .stl or .obj files from a 3D model.
FEA for finite element analysis
Digital Twin for adapting your finite element simulation to measured modal results
Result Viewer
Report for automatically generating report documents
Supported export types:
In FEA - Modal Analysis techniques from modal analysis are applied to the model of a structure to determine its vibration characteristics (natural frequencies and mode shapes). These characteristics are important parameters to understand dynamic loading conditions or as basis for transient or harmonic analysis.
The geometry is the starting point. Then on this geometry a mesh is generated. This mesh subdivides the geometry into elements that are used for the FEM analysis. Faces can be fixated as boundary conditions. Now the equations of motions are generated and solved providing natural frequencies and mode shapes. These results can then be animated on the provided geometry.
Results:
FEA Static allows simulation of static stress and strain. On the loaded geometry boundary conditions are set and a force or pressure is being applied. Then the module calculates and visualizes via a colormap on the geometry stress and strain in different directions.
Transient analysis is a technique used to determine the dynamic response of a structure under the action of any general time-dependent loads. This type of analysis can be used to determine the reaction of a structure as it responds to any combination of static, transient and harmonic loads.
WaveSim uses the Newmark time integration method to solve the basic equations of motion at discrete timepoints.
FEA Frequency Response Function Analysis is based on FEA Transient Analysis but goes one step further. After responses are estimated according to FEA Transient Analysis, frequency response functions (FRFs) are calculated between input channel and output channels. The mode shapes of these FRFs can then be visualized for different frequencies. The frequency response analysis is used for the calculation of amplitude, phase and frequency response.
Two methods are available:
The WaveSim FE Model Updating is a powerful tool for adapting your finite element simulation to measured modal results.
This will create a modal, digital twin of your structure. WaveSim FE Model Updating is designed to be easy to use and is a useful tool for newcomers to FE. It iteratively optimizes the material parameters of the simulation up to an exact reproduction of the modal characteristics of the measured structure.
Model Updating also provides semi-automatic geometry matching to adapt the geometries from the simulation to the measured geometry (image). This is an important step to achieve comparability of the results and is done semi-automatically.
For the first time, compare structural dynamic high-speed camera analyses with simulations and classical vibration sensors, such as accelerometers or laser vibrometers, and validate your measurements or simulations. By means of semi-automatic geometry matching, similarities between the results can be determined by determining the MAC criterion. By supporting the UFF file format, any modal result from different modal analysis software packages can be used.
WaveSim Report allows you to generate automatically detailed report documents. The report contains all important information about your measurement data, the measured object, photos, videos and of course the results of the analysis. You can design the report individually and, for example, save only relevant modes or include only certain measurement data as a plot. For the export of the report documents various formats are supported (*.docx, *.pptx, *.pdf).
